十个基础算法及其讲解

算法一:快速排序算法
快速排序是由东尼·霍尔所发展的一种排序算法。
在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n^2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
算法步骤
- 从数列中挑出一个元素,称为 “基准”(pivot)。
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
没仔细研究 QuickSort 前,一直以为 Partition 的实现大约存在两个版本:一个是 CLRS (算法导论)的实现(单方向一趟遍历,数据交换频繁),另一个是严蔚敏数据结构的实现(双方向进行,变换方向和数据)。
后来,看了不少资料(与后文所述的 BFPRT 相关)后,才知道原来严蔚敏书中所讲的 Partition 的实现来自 QuickSort 原作者,即 HOARE-PARTITION。
经过简单的测试发现,两种方法存在一倍的时间差距,也即双方向对数据序列遍历更高效。
示例代码
// 严蔚敏版数据结构实现方法,类似 C. A. R. Hoare 的实现
int partition(int *array, int low, int high)
{
int pivotkey = array[low];
while (low < high) {
while (low < high && array[high] >= pivotkey) {
high--;
}
if (low < high) {
array[low++] = array[high];
}
while (low < high && array[low] <= pivotkey) {
low++;
}
if (low < high) {
array[high--] = array[low];
}
}
array[low] = pivotkey;
return low; // 返回基准元素的下标
}
// CLRS 上面划分方法的实现
int partition2(int *array, int low, int high)
{
int pivotkey = array[high]; // 选取最后一个元素作为基准
int p = low - 1;
for (; low <= high; low++) {
if (array[low] <= array[high]) {
p++;
if (p != low) { // 在p前面的都是大于pivotkey的元素
swap(array, p, low); // 在p位置和其后的都是小于等于pivotkey的元素
}
}
}
return p;
}
// 快速排序的递归实现
void quicksort(int *array, int low, int high)
{
if (low < high) {
int mid = partition(array, low, high);
if (low < mid - 1) {
quicksort(array, low, mid - 1);
}
if (high > mid + 1) {
quicksort(array, mid + 1, high);
}
}
}
// 快速排序使用栈的非递归实现
void quicksort_nr(int *array, int low, int high)
{
if (low < high) {
int *stack = (int *) malloc((high - low + 1) * sizeof(int));
int p = 0;
int mid = partition(array, low, high);
if (low < mid - 1) {
stack[p++] = low;
stack[p++] = mid - 1;
}
if (high > mid + 1) {
stack[p++] = mid + 1;
stack[p++] = high;
}
// 其实就是用栈保存每一个待排序子串的首尾元素下标,
// 下一次while循环时取出这个范围,对这段子序列进行partition操作
while (p != 0) {
high = stack[--p];
low = stack[--p];
mid = partition(array, low, high);
if (low < mid - 1) {
stack[p++] = low;
stack[p++] = mid - 1;
}
if (high > mid + 1) {
stack[p++] = mid + 1;
stack[p++] = high;
}
}
free(stack);
}
}
算法二:堆排序算法
堆排序(Heap sort),是指利用堆这种数据结构所设计的一种排序算法。
堆积是一个近似完全二叉树的结构(二叉堆),并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
堆排序的平均时间复杂度为 Ο(NlogN)。
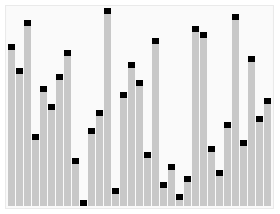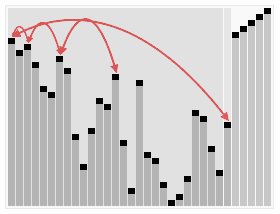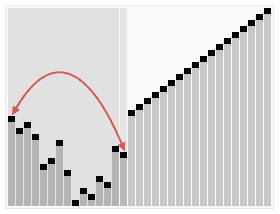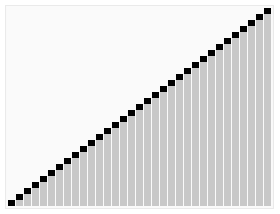
基本思想
- 先将初始文件 R[1..n] 建成一个大顶堆,此堆为初始的无序区
- 再将关键字最大的记录 R[1](即堆顶)和无序区的最后一个记录 R[n] 交换,由此得到新的无序区 R[1..n-1] 和有序区 R[n],且满足 R[1..n-1].keys≤R[n].key
- 由于交换后新的根 R[1] 可能违反堆性质,故应将当前无序区 R[1..n-1] 调整为堆。然后再次将 R[1..n-1] 中关键字最大的记录 R[1] 和该区间的最后一个记录 R[n-1] 交换,由此得到新的无序区 R[1..n-2] 和有序区 R[n-1..n],且仍满足关系 R[1..n-2].keys≤R[n-1..n].keys,同样要将 R[1..n-2] 调整为堆。
算法步骤
- 构建一个堆 H[0..n-1]。建堆是不断调整堆的过程,从 len/2 处(最后一个非叶节点)开始调整,一直到第一个节点,此处 len 是堆中元素的个数。建堆的过程是线性的过程,从 len/2 到 0 处一直调用调整堆的过程,相当于 o(h1)+o(h2)…+o(hlen/2) 其中 h 表示节点的深度,len/2 表示节点的个数,这是一个求和的过程,结果是线性的 O(N)。
- 把堆首(最大值)和堆尾互换。
- 把堆的尺寸缩小 1,调整堆,把新的数组顶端数据调整到相应位置。其思想是比较节点 i 和它的孩子节点 left(i)、right(i),选出三者最大(或者最小)值,如果最大(小)值不是节点 i 而是它的一个孩子节点,那边交互节点 i 和该节点,然后再调用调整堆过程,这是一个递归的过程。调整堆的过程时间复杂度与堆的深度有关系,是 logN 的操作,因为是沿着深度方向进行调整的。
- 重复步骤 2,直到堆的尺寸为 1。
示例代码
void swap(int *array, int a, int b)
{
if (a != b) {
array[a] = array[a] ^ array[b];
array[b] = array[a] ^ array[b];
array[a] = array[a] ^ array[b];
}
}
// 自顶向下建立大顶堆
void buildheap(int *data, int len)
{
int i = 0;
int parent = 0;
int child = 0;
int key_value = 0;
for (; i < len; ++i) {
child = i;
key_value = data[child];
for (; (parent = ((child + 1) >> 1) - 1) >= 0; child = parent) {
if (key_value > data[parent]) {
//swap(data, child, parent);
data[child] = data[parent];
} else {
break;
}
}
data[child] = key_value;
}
}
// 调整堆
void heapadjust(int *data, int parent, int len)
{
int child = 0;
int key_value = data[parent];
for (; (child = 2 * parent + 1) < len; parent = child) {
//child = 2 * parent + 1;
if (child < len-1 && data[child] < data[child+1]) {
child++;
}
if (key_value < data[child]) {
//swap(data, parent, child);
data[parent] = data[child];
} else {
break;
}
}
data[parent] = key_value;
}
void heapsort(int *data, int len)
{
int i = len/2 - 1;
for (; i >= 0; i--) {
heapadjust(data, i, len); // 自底向上建立大顶堆
}
//buildheap(data, len);
for (i=len-1; i > 0; i--) {
swap(data, 0, i);
heapadjust(data, 0, i);
}
}
算法三:归并排序
归并排序(Merge sort),是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
归并过程为:
比较 a[i] 和 a[j] 的大小,若 a[i]≤a[j],则将第一个有序表中的元素 a[i] 复制到 r[k] 中,并令 i 和 k 分别加上 1;
否则将第二个有序表中的元素 a[j] 复制到 r[k] 中,并令 j 和 k 分别加上 1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到 r 中从下标 k 到下标 t 的单元。
归并排序的算法我们通常用递归实现,先把待排序区间 [s,t] 以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间 [s,t]。

算法步骤
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤 3 直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
性能分析
- 归并排序,速度仅次于快速排序,是稳定的排序算法(相等元素的相对位置前后不会改变),适用于总体无序,但是各子项相对有序的数列。
- 时间复杂度,比较次数最好、最坏、平均时间都是 O(NlogN),与堆排序一样,而空间复杂度是 O(N),比较占用内存。
- 另一种用法,用来求逆序对数,在归并的过程中计算每个小区间的逆序对数,进而计算出大区间的逆序对数(也可以用树状数组来求解)。
(对于一个包含 N 个非负整数的数组 A[1…n],如果有 i < j,且 A[i] > A[j],则称 (A[i] ,A[j]) 为数组 A 中的一个逆序对。)
示例代码 (Java 实现便于书写)
A. 2-路归并 Merge 算法(优化)
/**
* @param source
* the array to be sorted
* @param buffer
* the temporary space for sorted data
* @param start
* the 1st partition's start position for source array
* @param mid
* the 1st partition's end position for source array
* @param end
* the 2nd partition's end position for source array
*/
private void merge(int[] source, int[] buffer, int start, int mid, int end) {
int i = start;
int k = start;
int j = mid + 1;
while (i <= mid && j < end + 1) {
if (source[i] > source[j]) {
buffer[k++] = source[j++];
} else {
buffer[k++] = source[i++];
}
}
// If the 1st partition doesn't go to the end, which means the 2nd partition has been merged to the buffer,
// then just need move the left data of the 1st partition to the right position, and no need copy to and
// then copy back again; but must consider the data overlapping.
// Otherwise, the 2nd partition's data is left and there is no sense to move or copy them.
if (i != mid + 1) {
// System.arraycopy(source, i, source, i + (end - mid), mid + 1 - i);
System.arraycopy(source, i, source, i + (j - mid - 1), mid - i + 1);
}
System.arraycopy(buffer, start, source, start, i - start + j - mid - 1);
// if (i != mid + 1) {
// while (i <= mid) {
// buffer[k++] = source[i++];
// }
// }
// System.arraycopy(buffer, start, source, start, i - start + j - mid - 1);
// if (i != mid + 1) {
// while (i <= mid) {
// buffer[k++] = source[i++];
// }
// }
// if (j != end + 1) {
// while (j <= end) {
// buffer[k++] = source[j++];
// }
// }
// System.arraycopy(buffer, start, source, start, end - start + 1);
// while (start <= end) {
// source[start] = buffer[start];
// start++;
// }
}
B. 递归归并算法(分治法:自顶向下)
/**
* @param array
* the source array
* @param temp
* the buffer array to store sorted data
* @param start
* the start position of target array
* @param end
* the end position of target array
*/
public void mergeSort(int[] array, int[] temp, int start, int end) {
if (start < end) {
int midIndex = (start + end) / 2;
mergeSort(array, temp, start, midIndex);
mergeSort(array, temp, midIndex + 1, end);
merge(array, temp, start, midIndex, end);
}
}
C. 归并算法(自底向上)
/**
* 若子文件个数为奇数,则最后一个子文件无须和其它子文件归并(即本趟轮空)
*
* 若子文件个数为偶数,则要注意最后一对子文件中后一子文件的区间上界是 n
*/
public void mergeSort2(int[] array, int[] temp, int n) {
int i = 0;
// 待排序的文件 R[1..n] 看作是 n 个长度为 1 的有序子文件
// 各子文件长度为 length (最后一个子文件的长度可能小于 length)
for (int length = 1; length < n; length *= 2) {
for (i = 0; i + 2 * length <= n; i += 2 * length) { // i+2*len-1<=n-1
this.merge(array, temp, i, i + length - 1, i + 2 * length - 1);
}
if (i + length < n) { // i+len-1<n-1
this.merge(array, temp, i, i + length - 1, n - 1);
// 尚有两个子文件,其中后一个长度小于length,归并最后两个子文件
// 注意:若i≤n-1且i+length-1≥n-1时,则剩余一个子文件轮空,无须归并
}
}
}
D. 非递归归并算法(堆栈)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public void mergeSortNoRecur(int[] array, int[] temp) {
int start = 0;
int end = array.length - 1;
if (start < end) {
int mid = (start + end) / 2;
Stack<Integer> indexStack = new Stack<Integer>();
indexStack.push(end);
indexStack.push(start);
while (!indexStack.isEmpty()) {
mid = start;
start = indexStack.pop();
if (mid == (start + indexStack.peek()) / 2 + 1) {
end = indexStack.pop();
this.merge(array, temp, start, mid - 1, end);
// Maybe the last two partition has been merged, so that
// the stack should be empty and certainly the sort work is finished.
if (indexStack.isEmpty()) {
break;
}
mid = start;
// Judge if need to traverse and divide the right child
start = indexStack.pop();
if (end == (start + indexStack.peek()) / 2) {
end = indexStack.peek();
indexStack.push(start);
mid = (start + end) / 2;
if (end > mid + 1) {
indexStack.push(end);
indexStack.push(mid + 1);
} else {
// If can't divide on the left side, then turn to the right side
start = mid + 1;
}
} else {
// Restore the previous value if don't divide the right child,
// which means should merge the last merge with another merge partition again
indexStack.push(start);
start = mid;
}
} else {
// Start to divide the left child
end = indexStack.peek();
indexStack.push(start);
mid = (start + end) / 2;
if (start < mid) {
indexStack.push(mid);
indexStack.push(start);
} else {
start = mid + 1;
}
}
}
}
}
E. 另一非递归归并算法(堆栈)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
// 非递归实现(感觉跟二叉树后序遍历的非递归实现很像)
void NonRecursiveMergeSort(int[] array, int[] temp, int len) {
Stack<Region> region_stack = new Stack<Region>();
Region beginRegion = new Region(0, len - 1, Type.PARTITION);
region_stack.push(beginRegion);
while (!region_stack.empty()) {
Region region = region_stack.pop(); // 从栈中删除
if (Type.MERGE.equals(region.getFlag())) {// 应该归并
this.merge(array, temp, region.getFirst(),
(region.getFirst() + region.getEnd()) / 2, region.getEnd());// 归并之
} else {// 应该划分
if (region.getFirst() + 1 >= region.getEnd()) {// 如果区域是两个相邻的数
this.merge(array, temp, region.getFirst(),
(region.getFirst() + region.getEnd()) / 2, region.getEnd());// 直接合并之
} else { // 否则应该划分
region.setFlag(Type.MERGE); // 下次应该归并
region_stack.push(region);
int mid = (region.getFirst() + region.getEnd()) / 2;
Region region_low = new Region(region.getFirst(), mid,
Type.PARTITION);
region_stack.push(region_low);
Region region_high = new Region(mid + 1, region.getEnd(),
Type.PARTITION);
region_stack.push(region_high);
}
}
}
}
public enum Type {
MERGE, // Need to merge
PARTITION // Need to divide
}
public class Region {
private final int first; // 起始位置
private final int end; // 结束位置
private Type flag; // 标记该区域是应该划分还是应该归并
private Region(int first, int end, Type flag) {
super();
this.first = first;
this.end = end;
this.flag = flag;
}
public int getFirst() {
return first;
}
public int getEnd() {
return end;
}
public Type getFlag() {
return flag;
}
public void setFlag(Type flag) {
this.flag = flag;
}
}
算法四:二分查找算法
二分查找算法是一种在有序数组中查找某一特定元素的搜索算法。搜素过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜素过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。折半搜索每次把搜索区域减少一半,时间复杂度为 Ο(logN)。
int binary_search(const int *array, const int n, int key)
{
int low = 0;
int high = n - 1;
int mid = 0;
while (low <= high) {
/*if (key == array[low]) {
return low;
}
if (key == array[high]) {
return high;
}*/
/*使用(low+high)/2会有整数溢出的问题
问题会出现在当low+high的结果大于表达式结果类型所能表示的最大值时,
这样,产生溢出后再/2是不会产生正确结果的,而low+((high-low)/2)不存在这个问题*/
mid = low + (high - low) / 2;
if (key == array[mid]) {
return mid;
}
if (key < array[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}
算法五:BFPRT(线性查找算法)
BFPRT 算法解决的问题十分经典,即从某n个元素的序列中选出第 k 小(第 k 大)的元素,通过巧妙的分析,BFPRT 可以保证在最坏情况下仍为线性时间复杂度。该算法的思想与快速排序思想相似,当然为使得算法在最坏情况下,依然能达到 O(n) 的时间复杂度,五位算法作者(Blum、Floyd、Pratt、Rivest、Tarjan)做了精妙的处理,该算法的简单和巧妙颇有我们需要借鉴学习之处。
算法刊登在Blum et al. (Tarjan),以论文作者名字首字母组合来命名。
http://en.wikipedia.org/wiki/Median_of_medians
算法步骤
- 将 n 个元素每 5 个一组,分成 n/5 (上界)组。
- 取出每一组的中位数,任意排序方法,比如插入排序。
- 递归的调用 select 算法查找上一步中所有中位数的中位数,设为 x,偶数个中位数的情况下设定为选取中间小的一个。
- 用 x 来分割数组,设小于等于 x 的个数为 m ,大于 x 的个数即为 n-m。
- 若 k==m,返回 x;若 k<m ,在小于 x 的元素中递归查找第 k 小的元素;若 k>m,在大于 x 的元素中递归查找第 k-m 小的元素。
终止条件:n=1 时,返回的即是 k 小元素。
个人的一点思考
递归调用单独寻找中位数的算法,得到的并不是中位数的中位数。
阅读这篇文章:http://www.johndcook.com/blog/2009/06/23/tukey-median-ninther/
这个算法看起来简单,似乎可以直接认为是快排改进快速选择。但真正理解这个算法后,才能通晓其高明之处,其思想绝对精华,不愧为“来自圣经的算法”。
然则要理解这个算法,也有一定的难度,其中有几个点要特别注意:
A. 划分方法的基准选取,即算法所讲的中位数的中位数,如何计算它更加高效 ?
B. 递归调用 Select 计算中位数的中位数(看起来复杂,实际可行),并非递归寻找中位数的方法
C. 将第一次找到的中位数集合交换到数组最左边,更方便递归寻找它们的中位数;花费额外空间存储中位数,递归返回是元素值,还需要额外 O(N) 的时间定位其下标;虽然与前者 Swap 的时间相抵消,但是空间的开销需要考虑
D. Select 返回值是元素值,而不是下标索引,Partition 基准参数也是下标;计算中位数的中位数过程,一定会将中位数放置到计算前设定的下标上
E. Partition 要保证一个值从原数据序列中隔离出来,不参与下次划分,这个值就是边界,同时也是第 i 小元素
Like RANDOMIZED-SELECT, the algorithm SELECT finds the desired element by recursively partitioning the input array. Here, however, we guarantee a good split upon partitioning the array. SELECT uses the deterministic partitioning algorithm PARTITION from quicksort (see Section 7.1), but modified to take the element to partition around as an input parameter.
The SELECT algorithm determines the ith smallest of an input array of n > 1 distinct elements by executing the following steps. (If n == 1, then SELECT merely returns its only input value as the ith smallest.)
- Divide the n elements of the input array into ⌊n / 5⌋ groups of 5 elements each and at most one group made up of the remaining n mod 5 elements.
- Find the median of each of the ⌉n / 5⌈ groups by first insertion-sorting the elements of each group (of which there are at most 5) and then picking the median from the sorted list of group elements.
- Use SELECT recursively to find the median x of the ⌉n / 5⌈ medians found in step 2. (If there are an even number of medians, then by our convention, x isthe lower median.)
- Partition the input array around the median-of-medians x using the modified version of PARTITION. Let k be one more than the number of elements on the low side of the partition, so that x is the kth smallest element and there are n - k elements on the high side of the partition.
- If i == k, then return x. Otherwise, use SELECT recursively to find the ith smallest element on the low side if i < k, or the (i - k)th smallest element on the high side if i > k.
性能分析
BFPRT 算法最出色的地方在于,精心设计的 pivot 选取方法,使得最坏情形理论上达到了线性时间复杂度。 这样找到的 pivot 能保证在这个 pivot 之前一定有至少 0.3N 的数,在这个 pivot 之后的也至少有 0.3N 的数,从而,每次 partition 不会出现数据倾斜(基本上整个数组都在 pivot 之后或者之前),由此保证了 pivot 的有效性(如下图)。理论分析这个算法的时间复杂度是 O(N) ,具体证明细节请参考算法导论。(由于常数比较大,实际效果并不一定好。)
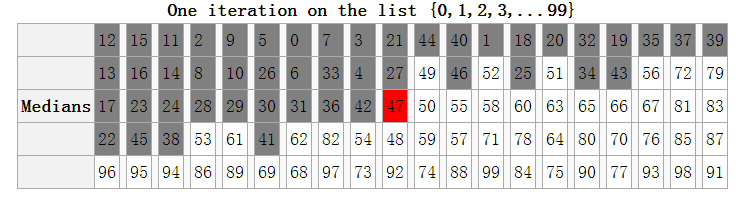
然而实际应用中,寻找中位数的中位数的时间开销很大,即便是 O(n) 平均查找时间,相比固定的选取 pivot 的 Quick-Select 算法,效率不但不高,反而很差。
博主亲测,双核 2.27 GHz CPU、x86架构、VS2010,随机产生 256MB 整型数据,选出第 14 小元素,BFPRT 算法花费CPU时间 1293756ms,而固定选择最低位作为 pivot 的 Quick-Select 算法仅需要 2603ms,而以三元素取中值作为 pivot 的 Quick-Select 时间为 12825ms。
由此可见,BFPRT 还不适合应用于实践,一般而言最坏情形发生的可能性还是比较低的,选择高效适宜的算法才是关键。
同样地,我们都知道快排和归并的平均时间复杂度都是 O(nlogn),但是实际应用中相比归并排序,快排耗费的时间更少;然而,对于链式存储结构的,我们还是倾向选择归并排序,原因就是快排在一趟划分过程中需要花费更多时间去定位元素,而归并排序需要额外的辅存空间,适用于链表结构。那么,对于顺序存储结构,快速排序就是优先选择了。
至于,为何利用 5 个元素作为元组大小,根据计算以 3 个元素分组有更好的数据平衡,有人认为与寄存器的数量和运算有关。
示例代码
在研究 BFPRT时, 看过不少人写的代码实现,有的忽略不足5个元素的那组;有的将分组后每组中位数前置,有的另为它们另分配内存;有的求中位数的中位数仅递归了Select方法的一部分,有的Partition写的让人很无语,有的写完了都没有测试过,……等等,千奇百怪,没见几个能完整的实现出来的(伪代码写的大有人在)。
偶尔发现一位对BFPRT分析的很不错,在这里:BFPRT算法
鉴于代码的鱼龙混杂,没有统一的思路,于是乎博主决定亲自写一个标准的实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
void insertsort(int *array_t, int start, int end)
{
for (int i = start; i <= end; i++) {
int inserted_data = array_t[i];
int j = i;
for (; j > start; j--) {
if (inserted_data < array_t[j - 1]) {
array_t[j] = array_t[j - 1];
} else {
break;
}
}
if (j != i) {
array_t[j] = inserted_data;
}
}
}
int partition(int *array_t, int low, int high, int pivot_index)
{
int pivot_value = array_t[pivot_index];
swap(array_t, low, pivot_index);
while (low < high) {
while (low < high && array_t[high] >= pivot_value) {
high--;
}
if (low < high) {
array_t[low++] = array_t[high];
}
while (low < high && array_t[low] <= pivot_value) {
low++;
}
if (low < high) {
array_t[high--] = array_t[low];
}
}
array_t[low] = pivot_value;
return low;
}
// 五划分中项:中位数的中位数(the median of medians algorithm)
// 严格依照 CLRS 算法描述实现,计算中位数的中位数时,没有忽略不足 5 个元素的那组数据
// Return the kth value
int select(int *array_t, int left, int right, int k)
{
const int k_group_size = 5;
int size = right - left + 1;
if (size <= k_group_size) {
insertsort(array_t, left, right);
return array_t[k + left - 1];
}
// (right - left) / 2 + left
const int num_group = (size % k_group_size) > 0 ? (size / k_group_size) + 1 : (size / k_group_size);
//int *medians_arr = new int[num_group];
for (int i = 0; i < num_group; i++) {
int sub_left = left + i * k_group_size;
int sub_right = sub_left + k_group_size - 1;
if (sub_right > right) {
sub_right = right;
}
insertsort(array_t, sub_left, sub_right);
// IMPORTANT !!
// Place these median in front of array_t, so as to recurse to find the median of median
int median = sub_left + ((sub_right - sub_left) >> 1);
swap(array_t, left + i, median);
//medians_arr[i] = array_t[sub_left + (sub_right - sub_left) >> 1];
// Better not to use new array to store the medians, otherwise have to traverse the array_t to find the pivot index due to select function returning pivot value.
}
// IMPORTANT !!
// Get the index of median
int pivot_index = left + ((num_group - 1) >> 1);
//int pivotValue = select(medians_arr, 0, num_group - 1, pivot_index);
// IMPORTANT !!
// Recurse to call and place the median on the pivot_index, without care about the median value
// Because the value of pivot_index must be the median after select function recursive call.
select(array_t, left, left + num_group - 1, (num_group + 1) >> 1);
int mid_index = partition(array_t, left, right, pivot_index);
int _ith = mid_index - left + 1;
// _ith_element == array_t[_ith]
if (k == _ith) {
return array_t[mid_index];
} else if (k < _ith) {
return select(array_t, left, mid_index - 1, k);
} else {
return select(array_t, mid_index + 1, right, k - _ith);
}
}
算法六:DFS(深度优先搜索)
深度优先搜索算法(Depth-First-Search),是搜索算法的一种。
它沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所有边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。DFS属于盲目搜索。
深度优先搜索是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。
深度优先遍历图算法步骤:
- 访问顶点v;
- 依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
- 若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
上述描述可能比较抽象,举个实例:
DFS 在访问图中某一起始顶点 v 后,由 v 出发,访问它的任一邻接顶点 w1;再从 w1 出发,访问与 w1邻 接但还没有访问过的顶点 w2;然后再从 w2 出发,进行类似的访问,… 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点 u 为止。
接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点。如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止。
算法七:BFS(广度优先搜索)
广度优先搜索算法(Breadth-First-Search),是一种图形搜索算法。
简单的说,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止。BFS同样属于盲目搜索。一般用队列数据结构来辅助实现BFS算法。
算法步骤:
- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。 如果找到目标,则结束搜寻并回传结果; 否则将它所有尚未检验过的直接子节点加入队列中。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
- 重复步骤2。
DFS & BFS 示例代码
以二叉树为例,分别进行深度优先遍历和广度优先遍历;最后实现一个栈空间 O(1) 的非递归算法 —— Morris 遍历,它的本质就是线索二叉树。
A. 递归建立、销毁二叉树
// define tree, stack and queue structure
typedef struct tree_node {
int data;
struct tree_node *left, *right;
} tree_node;
typedef struct nodestack {
tree_node *node;
struct nodestack *below;
} nodestack;
typedef struct nodequeue {
tree_node *node;
struct nodequeue *rear;
} nodequeue;
// Set up and destroy binary tree
void create_binary_tree(tree_node **tree_root)
{
int data;
char ch;
// eg. {1024 37 2 0$ 0$ 936 80 0$ 0$ 768 0$ 0$ 9 131 0$ 0$ 0$}
scanf("%d%c", &data, &ch);
if ('$' == ch) {
(*tree_root) = NULL;
} else {
(*tree_root) = (tree_node *) malloc(sizeof(tree_node));
(*tree_root)->data = data;
create_binary_tree(&((*tree_root)->left));
create_binary_tree(&((*tree_root)->right));
}
}
void destroy_binary_tree(tree_node *tree_root) {
if (NULL != tree_root) {
destroy_binary_tree(tree_root->left);
destroy_binary_tree(tree_root->right);
free(tree_root);
}
}
B. 深度优先遍历(递归、非递归;前序、中序、后序)
// Depth_First Search
// traverse binary tree recursively
void traverse(tree_node *root)
{
if (NULL != root) {
printf("%d ", root->data); // preorder_traverse
traverse(root->left);
// printf ==> inorder_traverse
traverse(root->right);
// printf ==> postorder_traverse
}
}
// traverse non-recursively using stack
void traverse_nr(tree_node *root)
{
nodestack *st = NULL;
while (NULL != root || NULL != st) {
if (NULL != root) {
// Push into stack
printf("%d ", root->data); // preorder_traverse
nodestack *el = (nodestack *) malloc(sizeof(nodestack));
el->node = root;
el->below = st;
st = el;
root = root->left;
} else {
// Pop from the stack
nodestack *top = st;
// printf ==> inorder_traverse
root = top->node->right;
st = st->below;
free(top);
}
}
}
void postorder_traverse_nr(tree_node *root)
{
nodestack *st = NULL;
tree_node *cur = root;
tree_node *prev = NULL;
while (NULL != cur || NULL != st) {
if (NULL != cur) {
nodestack *el = (nodestack *) malloc(sizeof(nodestack));
el->node = cur;
el->below = st;
st = el;
cur = cur->left;
} else {
cur = st->node;
if (cur->right == prev || cur->right == NULL) {
printf("%d ", cur->data); // postorder_traverse
prev = cur;
cur = NULL;
nodestack *top = st;
st = st->below;
free(top);
} else {
cur = cur->right;
}
}
}
}
C. Morris 遍历算法(中序遍历)
// Morris Algorithms for inorder-traverse
void inorder_traverse_mo(tree_node *root)
{
while (NULL != root) {
if (NULL == root->left) {
printf("%d ", root->data);
root = root->right;
} else {
tree_node *cur = root->left;
while (NULL != cur->right && root != cur->right) {
cur = cur->right;
}
if (NULL == cur->right) { // the 1st visit, change the right pointer to successor
cur->right = root;
root = root->left;
} else { // the 2nd visit, restore the right pointer to NULL
cur->right = NULL;
printf("%d ", root->data);
root = root->right;
}
}
}
}
D. 广度优先遍历
// Breadth_First Search
// traverse binary tree by level layer
void level_traverse(tree_node *root)
{
if (NULL != root) {
nodequeue *head = (nodequeue *) malloc(sizeof(nodequeue));
head->node = root;
head->rear = NULL;
nodequeue *tail = head;
nodequeue *el = NULL;
while (NULL != head) {
printf("%d ", head->node->data);
if (NULL != head->node->left) {
el = (nodequeue *) malloc(sizeof(nodequeue));
el->node = head->node->left;
el->rear = NULL;
tail->rear = el;
tail = el;
}
if (NULL != head->node->right) {
el = (nodequeue *) malloc(sizeof(nodequeue));
el->node = head->node->right;
el->rear = NULL;
tail->rear = el;
tail = el;
}
nodequeue *ob_el = head;
head = head->rear;
free(ob_el);
}
}
}
算法八:Dijkstra 算法
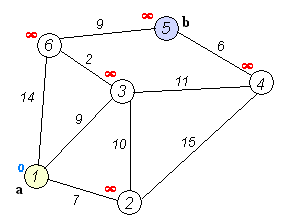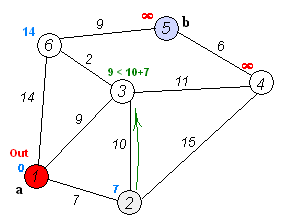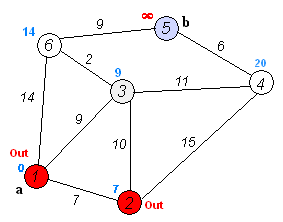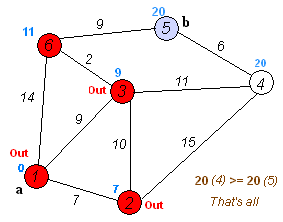
戴克斯特拉算法(Dijkstra’s algorithm)是由荷兰计算机科学家艾兹赫尔·戴克斯特拉提出。迪科斯彻算法使用了广度优先搜索解决非负权有向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
该算法的输入包含了一个有权重的有向图 G,以及G中的一个来源顶点 S。我们以 V 表示 G 中所有顶点的集合。每一个图中的边,都是两个顶点所形成的有序元素对。(u, v) 表示从顶点 u 到 v 有路径相连。我们以 E 表示G中所有边的集合,而边的权重则由权重函数 w: E → [0, ∞] 定义。因此,w(u, v) 就是从顶点 u 到顶点 v 的非负权重(weight)。边的权重可以想像成两个顶点之间的距离。任两点间路径的权重,就是该路径上所有边的权重总和。已知有 V 中有顶点 s 及 t,Dijkstra 算法可以找到 s 到 t的最低权重路径(例如,最短路径)。这个算法也可以在一个图中,找到从一个顶点 s 到任何其他顶点的最短路径。对于不含负权的有向图,Dijkstra 算法是目前已知的最快的单源最短路径算法。
算法步骤
- 初始时令 S={V0},T={其余顶点},T中顶点对应的距离值 若存在 <V0,Vi>,d(V0,Vi) 为 <V0,Vi> 弧上的权值; 若不存在 <V0,Vi>,d(V0,Vi) 为 ∞
- 从 T 中选取一个其距离值为最小的顶点 W 且不在 S 中,加入 S
- 对其余 T 中顶点的距离值进行修改:若加进 W 作中间顶点,从 V0 到 Vi 的距离值缩短,则修改此距离值(松弛操作)
重复上述步骤 2、3,直到 S 中包含所有顶点,即 W==Vi 为止
示例代码
#define INFINITE (~(0x1<<31)) // 最大值(即0X7FFFFFFF)
#define MAX_VERTEX_NUM 100 // 最大顶点个数
typedef enum BOOLEAN {
TRUE, FALSE
};
typedef struct MGraph {
char vexs[MAX_VERTEX_NUM]; // 顶点向量
int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵
int vexnum, arcnum; // 顶点数和弧数
} MGraph;
/************************************************************************/
/* Dijkstra 算法
* 统计图(G)中"顶点vs"到其它各个顶点的最短路径。
*
* Param:
* G -- 图
* v0 -- 起点
* path -- 每个终点的前一个顶点
* dist -- 起点到终点的最短路径
*/
/************************************************************************/
void shortest_path_dij(MGraph G, int v0, int path[], int dist[])
{
int vlen = G.vexnum;
int v = 0;
int i = 0;
int w = 0;
int min = INFINITE;
// flag[i] = TRUE 表示"顶点v0"到"顶点i"
BOOLEAN *flag = (BOOLEAN *) malloc(vlen * sizeof(BOOLEAN));
for (; v < vlen; ++v) {
flag[v] = FALSE;
dist[v] = G.arcs[v0][v];
if (INFINITE == G.arcs[v0][v]) {
path[v] = -1;
} else {
path[v] = v0;
}
}
flag[v0] = TRUE;
dist[v0] = 0;
for (i = 1; i < vlen; ++i) {
min = INFINITE;
for (v = 0; v < vlen; ++v) {
if (FALSE == flag[v] && min > dist[v]) {
min = dist[v];
w = v;
}
}
if (INFINITE == min) {
break;
}
flag[w] = TRUE;
for (v = 0; v < vlen; ++v) {
// 防止溢出
if (FALSE == flag[v] && INFINITE != G.arcs[w][v] && min + G.arcs[w][v] < dist[v]) {
dist[v] = min + G.arcs[w][v];
path[v] = w;
}
}
}
free(flag);
// 打印dijkstra最短路径的结果
/* printf("dijkstra(%c): \n", G.vexs[v0]);
for (i = 0; i < G.vexnum; i++) {
printf(" shortest(%c, %c) =", G.vexs[v0], G.vexs[i]);
if (INFINITE == dist[i]) {
printf(" ∞");
} else {
printf(" %d", dist[i]);
}
w = path[i];
if (w != -1) {
printf(" \tpath(%c, %c): ", G.vexs[i], G.vexs[v0]);
printf("%c <- ", G.vexs[i]);
while (w != -1 && w != v0) {
printf("%c <- ", G.vexs[w]);
w = path[w];
}
printf("%c", G.vexs[v0]);
}
printf("\n");
} */
}
备注:Dijkstra 算法用于求解单源、无负权图的最短路径,不能用于有负权图;
设想图中存在一个回路(从 v 出发,经过若干个节点后又回到 v)且这个回路中的所有边的权值之和为负;那么这个回路中任意两点的最短路径便可以无穷小下去,如果不处理负权回路的话,程序就会永远执行下去。
另一种算法,Bellman-Ford 算法具有识别这种负权回路的能力,可以判断有无负权回路(若有,则不存在最短路径)。它允许图中存在负权边,只要不存在从源点可达的负权回路即可;简单的说,图中可以存在负权边,但此条负权边,构不成负权回路,不影响回路的形成。
此外,SPFA 算法(Bellman-Ford 的队列优化)同样可以用于存在负数边权的图。
算法九:动态规划算法
动态规划(Dynamic Programming)是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
关于动态规划最经典的问题当属背包问题。
适用情况
能采用动态规划求解的问题的一般要具有3个性质:
- 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。最优子结构性质为动态规划算法解决问题提供了重要线索。
- 无后效性。即将各阶段按照一定的次序排列好之后,某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
- 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。
示例问题
A. 最大子数组和问题
题目:
由 N 个整数元素组成的一维数组 (A[0], A[1],…,A[n-1], A[n]),这个数组有很多连续子数组,那么其中数组之和的最大值是什么呢?
例如,数组 int A[5] = {-1, 2, 3, -4, 2};
符合条件的子数组为 {2, 3},即答案为 5;
这是一道很简单的题目,但是要想写出时间复杂度为 O(n) 的最优解法还是需要仔细推敲下的。
明确一下题意:
- 子数组必须是连续的。
- 不需要返回子数组的具体位置。
- 数组中包含:正整数,零,负整数。
例如:
数组:{1, -2, 3, 5, -3, 2} 返回值为 8
数组:{0, -2, 3, 5, -1, 2} 返回值为 9
数组:{-9, -2, -3, -5, -6} 返回值为 -2
分析:
首先,我们看看最直接的穷举法:
int MaxSubArray(int *A, int n)
{
int max = (0x1 << 31); //初始值为负无穷大
int sum, i, j;
for (i = 0; i < n; i++) {
sum = 0;
for (j = i; j < n; j++) {
sum += A[j];
if (sum > max) {
max = sum;
}
}
}
return max;
}
这种方法最直接,当然也是最耗时的,时间复杂度为 O(n^2);
可以优化吗?答案是肯定的,可以考虑数组的第一个元素 A[0] 和最大的一段子数组 (A[i], …, A[j]) 的关系,有以下几种情况:
- 当 0 = i = j 时,元素 A[0] 本身构成和最大的子数组;
- 当 0 = i < j 时,最大子数组以 A[0] 开始;
- 当 0 < i 时, 元素 A[0] 和最大子数组没有关系。
从上面3种情况可以看出:
可以将一个大问题(N个元素数组)转化为一个较小的问题(N-1个元素的数组)。
假设已经知道 (A[1], …, A[n-1]) 中和最大的一段子数组之和为 MaxArr[1],并且已经知道 (A[1],…,A[n-1]) 中包含 A[1] 的和最大的一段数组为 Start[1]。
那么不难看出 (A[0], …, A[n]) 中问题的解:MaxArr[0] = max{ A[0], A[0] + Start[1], MaxArr[1] }。
通过这样的分析,可以看出这个问题可以用动态规划来解决。
解决方案:
#define MAX(x, y) ((x) > (y) ? (x) : (y))
int MaxSubArray(int *A, int n)
{
int start = A[n - 1];
int max_arr_sum = A[n - 1];
int i;
for (i = n - 2; i >= 0; --i) { // 从后向前遍历,反之亦可
start = MAX(A[i], start + A[i]);
max_arr_sum = MAX(start, max_arr_sum);
}
return max_arr_sum; // max_arr_sum 中存放结果
}
由此看出,通过动规算法解决该问题,不仅效率很高(时间复杂度为O(n)),而且极其简便。
B. 0-1 背包问题
题目:
这题非常有名,只要是计算机专业的应该都有听说过。有 N 件物品和一个容量为 C 的背包;第 i 件物品的体积是 c[i],价值是 v[i]。求解将哪些物品装入背包可使价值总和最大。
把题目具体下,有 5 个物品,背包的体积为 10,物品的体积分别为 c[5] = { 3, 5, 2, 7, 4 },价值为 v[5] = { 2, 4, 1, 6, 5 }。
分析:
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。可以将背包问题的求解看作是进行一系列的决策过程,即决定哪些物品应该放入背包,哪些不放入背包。
如果一个问题的最优解包含了物品 n,即 Xn = 1,那么其余 X1, X2, ….., Xn-1 一定构成子问题 1,2,…..,n-1 在容量 C - Cn 时的最优解;
如果这个最优解不包含物品 n,即 Xn = 0,那么其余 X1, X2….., Xn-1 一定构成了子问题 1,2,….,n-1 在容量 C 时的最优解。(请仔细品味这几句话)
根据以上分析最优解的结构,递归定义问题的最优解: f[i][j] = max{ f[i-1][j], f[i-1][j - c[i]] + v[i] },其中 f[i][j] 表示 将 i 个物品放入体积为 j 的背包可获得的最大价值。
解决方案:
#define N 5
#define C 10
int c[N + 1] = {0,3,5,2,7,4};
int v[N + 1] = {0,2,4,1,6,5};
int f[N + 1][C + 1] = {0};
// f[i][j] = max{ f[i-1][j] , f[i-1][j - c[i]] + v[i]}
int main()
{
int i, j;
for (i = 1; i <= N; i++) {
for (j = 1; j <= C; j++) {
if (c[i] > j) { // 如果背包的容量,放不下c[i],则不选c[i]
f[i][j] = f[i - 1][j];
} else {
f[i][j] = MAX(f[i-1][j], f[i-1][j - c[i]] + v[i]); // 转移方程式
}
}
}
printf("The maximum value: %d\n", f[N][C]);
return 0;
}
0-1 背包问题是最基本的动态规划问题,也是最经典,最易懂的,它包含了背包问题中设计状态、方程的最基本思想。
算法十:朴素贝叶斯分类算法
朴素贝叶斯分类算法是一种基于贝叶斯定理的简单概率分类算法。贝叶斯分类的基础是概率推理,就是在各种条件的存在不确定,仅知其出现概率的情况下,如何完成推理和决策任务。概率推理是与确定性推理相对应的。而朴素贝叶斯分类器是基于独立假设的,即假设样本每个特征与其他特征都不相关。
朴素贝叶斯分类器依靠精确的自然概率模型,在有监督学习的样本集中能获取得非常好的分类效果。在许多实际应用中,朴素贝叶斯模型参数估计使用最大似然估计方法,换言之朴素贝叶斯模型能工作并没有用到贝叶斯概率或者任何贝叶斯模型。
实际中的表现,朴素贝叶斯方法往往并不比贝叶斯网络、决策树效果差,而且速度还很快。尽管是带着这些朴素思想和过于简单化的假设,但朴素贝叶斯分类器在很多复杂的现实情形中仍能够取得相当好的效果。
贝叶斯定理
| **P(A | B) = P(B | A) P(A) / P(B)** ,是关于随机事件 A 和 B 的条件概率和边缘概率的一则定理。其中: |
- P(A) :是 A 的先验概率或边缘概率。之所以称为”先验”是因為它不考虑任何 B 方面的因素。
-
P(A B) :是在 B 发生的情况下 A 发生的可能性。 - P(B) :是 B 的先验概率或边缘概率,也作标准化常量(normalized constant)。
| 定理可表述为:后验概率 = (相似度*先验概率) / 标准化常量,也就是說,后验概率与先验概率和相似度的乘积成正比。另外,**P(B | A) / P(B)** 也有时被称作标准相似度(standardised likelihood),Bayes 定理可表述为:后验概率 = 标准相似度 * 先验概率。 |
朴素贝叶斯分类器的公式
贝叶斯分类器的基本方法:
在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。假设某个体有 n 项特征(Feature),分别为 F1、F2、…、Fn。现有 m 个类别(Category),分别为 C1、C2、…、Cm。贝叶斯分类器就是计算出概率最大的那个分类,也就是求下面这个算式的最大值:
# P(F1,F2,...,Fn) 对于不同的类别都是相同的,作为常数忽略处理
# 再根据联合概率展开公式
P(C|F1,F2,...,Fn) = P(C) * P(F1,F2,...,Fn|C)
= P(C) * P(F1|C) * P(F2|F1,C) * ... * P(Fn|Fn-1,...,F1,C)
假设所有特征都彼此独立,公式简化为:
P(C|F1,F2,...,Fn) = P(C) * P(F1|C) * P(F2|C) * ... * P(Fn|C)
上式等号右边的每一项,都可以从统计资料中得到,由此就可以计算出每个类别对应的概率,从而找出最大概率的那个类。
分类器工作流程
整个朴素贝叶斯分类分为三个阶段,分类的流程可以由下图表示(暂时不考虑验证):
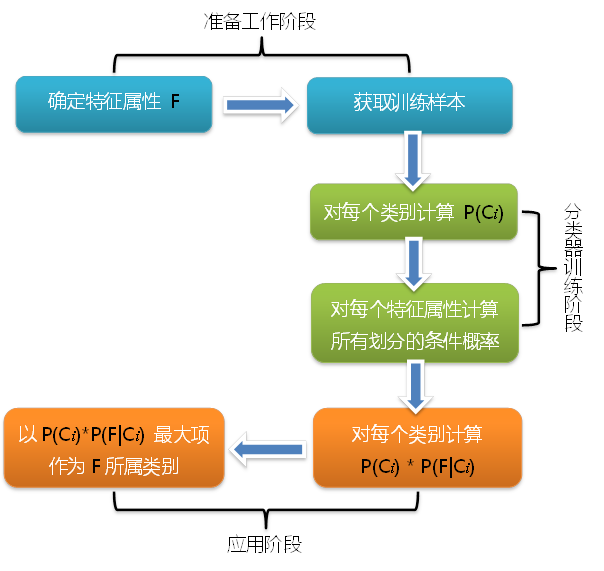
- 第一阶段——准备工作阶段
这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性 (F1,F2,…,Fn),并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类 (C1,C2,…,Cm),形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。 - 第二阶段——分类器训练阶段
这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率 P(Cj) 及每个特征属性划分对每个类别的条件概率估计 P(Fi|Cj),并将结果记录。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。 - 第三阶段——应用阶段
这个阶段的任务是使用分类器对待分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
贝叶斯分类器特点
朴素贝叶斯分类器的一个优势在于只需要根据少量的训练数据估计出必要的参数(变量的均值和方差)。由于变量独立假设,只需要估计各个变量的方法,而不需要确定整个协方差矩阵。
- 需要知道先验概率
先验概率是计算后验概率的基础。在传统的概率理论中,先验概率可以由大量的重复实验所获得的各类样本出现的频率来近似获得,其基础是“大数定律”,这一思想称为“频率主义”。而在称为“贝叶斯主义”的数理统计学派中,他们认为时间是单向的,许多事件的发生不具有可重复性,因此先验概率只能根据对置信度的主观判定来给出,也可以说由“信仰”来确定。 - 按照获得的信息对先验概率进行修正
在没有获得任何信息的时候,如果要进行分类判别,只能依据各类存在的先验概率,将样本划分到先验概率大的一类中。而在获得了更多关于样本特征的信息后,可以依照贝叶斯公式对先验概率进行修正,得到后验概率,提高分类决策的准确性和置信度。 - 分类决策存在错误率
由于贝叶斯分类是在样本取得某特征值时对它属于各类的概率进行推测,并无法获得样本真实的类别归属情况,所以分类决策一定存在错误率,即使错误率很低,分类错误的情况也可能发生。

[Comments]: